7.3.2 Tangential Cubic Splines
| Topic Version | 1 | Published | 09/11/2015 | |
| For Standard | RESQML v2.0.1 | |||
For tangential cubic splines, the control points and the tangential derivatives 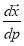 , are specified
at each knot. The function is everywhere continuous and differentiable, but the second
derivatives may be discontinuous at the knots. Using the cubic functional form within an
interval, these four constraints may be used to determine the second derivatives at the
interval edges.
, are specified
at each knot. The function is everywhere continuous and differentiable, but the second
derivatives may be discontinuous at the knots. Using the cubic functional form within an
interval, these four constraints may be used to determine the second derivatives at the
interval edges.
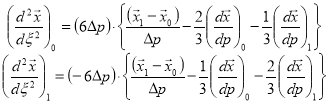
Hence:
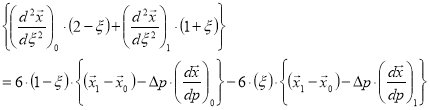
Notice that when written in this form, that zero values for Δp are permitted. This type of spline appears in many interactive graphics packages to provide a smooth interpolant with specified slopes at the knots.