7.3.1 Cubic Splines
| Topic Version | 1 | Published | 09/11/2015 | |
| For Standard | RESQML v2.0.1 | |||
There are many ways to describe a cubic spline. The current description draws heavily upon
the description in Numerical Recipes (Press et al. 1992), but with some variations that are in
use within our domain. For a spline, each interval 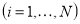 is parameterized
in terms of a parameter p, or equivalently a normalized parameter
is parameterized
in terms of a parameter p, or equivalently a normalized parameter ,
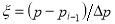 ,
,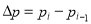 . The parameter
takes on the values of
. The parameter
takes on the values of =0 and
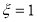 at the two knots that bound the interval. We may express a cubic
spline in terms of its function values and second derivatives, specified at the two knots.
Spline derivatives are specified with respect to the parameter p, but need to be converted to
a derivative with respect to within an interval,
at the two knots that bound the interval. We may express a cubic
spline in terms of its function values and second derivatives, specified at the two knots.
Spline derivatives are specified with respect to the parameter p, but need to be converted to
a derivative with respect to within an interval, 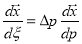 and
and 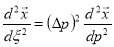 , when using the
following table of basis functions. Although the derivatives with respect to the parameter p
may be continuous at the knots, because of the scaling by Δp, the normalized derivatives
with respect to
, when using the
following table of basis functions. Although the derivatives with respect to the parameter p
may be continuous at the knots, because of the scaling by Δp, the normalized derivatives
with respect toneed not be. The interpolant for a cubic spline can then be written as a superposition of
four basis functions (Figure 7.3.1-1 ).
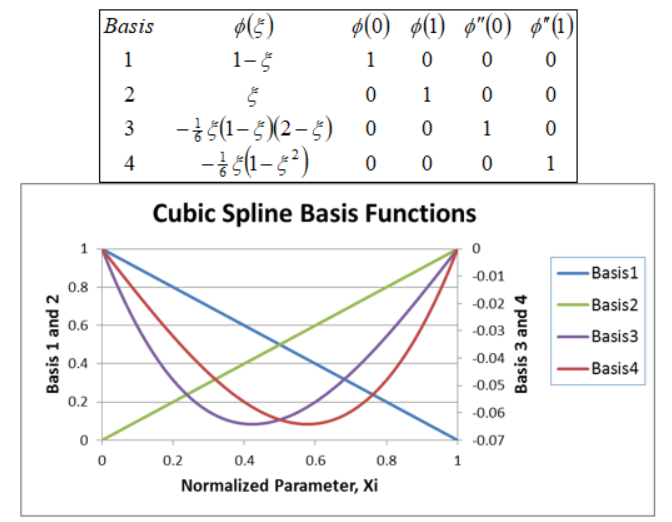
Specifically, within an interval we have:
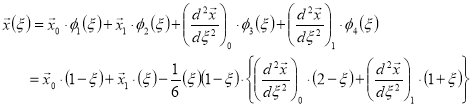
For instance, a function that takes on the values of a and b at the interval knots but with
vanishing second derivatives would be given by  . With non-zero
second derivatives, a cubic equation would arise. Any cubic spline may be expressed in this
fashion, and all cubic splines rely upon the specification of the control points at the knots.
However, different cubic spline implementations arise depending upon the specification of the
derivatives at the knots.
. With non-zero
second derivatives, a cubic equation would arise. Any cubic spline may be expressed in this
fashion, and all cubic splines rely upon the specification of the control points at the knots.
However, different cubic spline implementations arise depending upon the specification of the
derivatives at the knots.